Algorithms Reference Classification
Multinomial Logistic Regression
Description
The MultiLogReg.dml script performs both binomial and multinomial
logistic regression. The script is given a dataset $(X, Y)$ where matrix
$X$ has $m$ columns and matrix $Y$ has one column; both $X$ and $Y$ have
$n$ rows. The rows of $X$ and $Y$ are viewed as a collection of records:
$(X, Y) = (x_i, y_i)_{i=1}^n$ where $x_i$ is a numerical vector of
explanatory (feature) variables and $y_i$ is a categorical response
variable. Each row $x_i$ in $X$ has size $\dim x_i = m$, while its corresponding $y_i$
is an integer that represents the observed response value for
record $i$.
The goal of logistic regression is to learn a linear model over the feature vector $x_i$ that can be used to predict how likely each categorical label is expected to be observed as the actual $y_i$. Note that logistic regression predicts more than a label: it predicts the probability for every possible label. The binomial case allows only two possible labels, the multinomial case has no such restriction.
Just as linear regression estimates the mean value $\mu_i$ of a numerical response variable, logistic regression does the same for category label probabilities. In linear regression, the mean of $y_i$ is estimated as a linear combination of the features: $\mu_i = \beta_0 + \beta_1 x_{i,1} + \ldots + \beta_m x_{i,m} = \beta_0 + x_i\beta_{1:m}$. In logistic regression, the label probability has to lie between 0 and 1, so a link function is applied to connect it to $\beta_0 + x_i\beta_{1:m}$. If there are just two possible category labels, for example 0 and 1, the logistic link looks as follows:
\[Prob[y_i\,{=}\,1\mid x_i; \beta] \,=\, \frac{e^{\,\beta_0 + x_i\beta_{1:m}}}{1 + e^{\,\beta_0 + x_i\beta_{1:m}}}; \quad Prob[y_i\,{=}\,0\mid x_i; \beta] \,=\, \frac{1}{1 + e^{\,\beta_0 + x_i\beta_{1:m}}}\]Here category label 0 serves as the baseline, and function $\exp(\beta_0 + x_i\beta_{1:m})$ shows how likely we expect to see “$y_i = 1$” in comparison to the baseline. Like in a loaded coin, the predicted odds of seeing 1 versus 0 are $\exp(\beta_0 + x_i\beta_{1:m})$ to 1, with each feature $x_{i,j}$ multiplying its own factor $\exp(\beta_j x_{i,j})$ to the odds. Given a large collection of pairs $(x_i, y_i)$, $i=1\ldots n$, logistic regression seeks to find the $\beta_j$’s that maximize the product of probabilities $Prob[y_i\mid x_i; \beta]$ for actually observed $y_i$-labels (assuming no regularization).
Multinomial logistic regression [Agresti2002] extends this link to $k \geq 3$ possible categories. Again we identify one category as the baseline, for example the $k$-th category. Instead of a coin, here we have a loaded multisided die, one side per category. Each non-baseline category $l = 1\ldots k\,{-}\,1$ has its own vector $(\beta_{0,l}, \beta_{1,l}, \ldots, \beta_{m,l})$ of regression parameters with the intercept, making up a matrix $B$ of size $(m\,{+}\,1)\times(k\,{-}\,1)$. The predicted odds of seeing non-baseline category $l$ versus the baseline $k$ are $\exp\big(\beta_{0,l} + \sum\nolimits_{j=1}^m x_{i,j}\beta_{j,l}\big)$ to 1, and the predicted probabilities are:
\[\begin{equation} l < k: Prob [y_i {=} l \mid x_i; B] \,\,\,{=}\,\,\, \frac{\exp\big(\beta_{0,l} + \sum\nolimits_{j=1}^m x_{i,j}\beta_{j,l}\big)}{1 \,+\, \sum_{l'=1}^{k-1}\exp\big(\beta_{0,l'} + \sum\nolimits_{j=1}^m x_{i,j}\beta_{j,l'}\big)}; \end{equation}\] \[\begin{equation} Prob [y_i {=} k \mid x_i; B] \,\,\,{=}\,\,\, \frac{1}{1 \,+\, \sum_{l'=1}^{k-1}\exp\big(\beta_{0,l'} + \sum\nolimits_{j=1}^m x_{i,j}\beta_{j,l'}\big)}. \end{equation}\]The goal of the regression is to estimate the parameter matrix $B$ from the provided dataset $(X, Y) = (x_i, y_i)_{i=1}^n$ by maximizing the product of $Prob[y_i\mid x_i; B]$ over the observed labels $y_i$. Taking its logarithm, negating, and adding a regularization term gives us a minimization objective:
\[\begin{equation} f(B; X, Y) \,\,=\,\, -\sum_{i=1}^n \,\log Prob[y_i\mid x_i; B] \,+\, \frac{\lambda}{2} \sum_{j=1}^m \sum_{l=1}^{k-1} |\beta_{j,l}|^2 \,\,\to\,\,\min \end{equation}\]The optional regularization term is added to mitigate overfitting and degeneracy in the data; to reduce bias, the intercepts $\beta_{0,l}$ are not regularized. Once the $\beta_{j,l}$’s are accurately estimated, we can make predictions about the category label $y$ for a new feature vector $x$ using Eqs. (1) and (2).
Table 5
: The Log file for multinomial logistic regression
contains the following iteration variables in CSV format, each line
containing triple (Name, Iteration#, Value) with Iteration# being 0
for initial values.
| Name | Meaning |
|---|---|
| LINEAR_TERM_MIN | The minimum value of $X$ %*% $B$, used to check for overflows |
| LINEAR_TERM_MAX | The maximum value of $X$ %*% $B$, used to check for overflows |
| NUM_CG_ITERS | Number of inner (Conj. Gradient) iterations in this outer iteration |
| IS_TRUST_REACHED | $1 = {}$trust region boundary was reached, $0 = {}$otherwise |
| POINT_STEP_NORM | L2-norm of iteration step from old point (matrix $B$) to new point |
| OBJECTIVE | The loss function we minimize (negative regularized log-likelihood) |
| OBJ_DROP_REAL | Reduction in the objective during this iteration, actual value |
| OBJ_DROP_PRED | Reduction in the objective predicted by a quadratic approximation |
| OBJ_DROP_RATIO | Actual-to-predicted reduction ratio, used to update the trust region |
| IS_POINT_UPDATED | $1 = {}$new point accepted; $0 = {}$new point rejected, old point restored |
| GRADIENT_NORM | L2-norm of the loss function gradient (omitted if point is rejected) |
| RUST_DELTA | Updated trust region size, the “delta” |
Details
We estimate the logistic regression parameters via L2-regularized negative log-likelihood minimization (3). The optimization method used in the script closely follows the trust region Newton method for logistic regression described in [Lin2008]. For convenience, let us make some changes in notation:
- Convert the input vector of observed category labels into an indicator matrix $Y$ of size $n \times k$ such that $Y_{i, l} = 1$ if the $i$-th category label is $l$ and $Y_{i, l} = 0$ otherwise.
- Append an extra column of all ones, i.e. $(1, 1, \ldots, 1)^T$, as the $m\,{+}\,1$-st column to the feature matrix $X$ to represent the intercept.
- Append an all-zero column as the $k$-th column to $B$, the matrix of regression parameters, to represent the baseline category.
- Convert the regularization constant $\lambda$ into matrix $\Lambda$ of the same size as $B$, placing 0’s into the $m\,{+}\,1$-st row to disable intercept regularization, and placing $\lambda$’s everywhere else.
Now the ($n\,{\times}\,k$)-matrix of predicted probabilities given by (1) and (2) and the objective function $f$ in (3) have the matrix form
\[\begin{aligned} P \,\,&=\,\, \exp(XB) \,\,/\,\, \big(\exp(XB)\,1_{k\times k}\big)\\ f \,\,&=\,\, - \,\,{\textstyle\sum} \,\,Y \cdot (X B)\, + \, {\textstyle\sum}\,\log\big(\exp(XB)\,1_{k\times 1}\big) \,+ \, (1/2)\,\, {\textstyle\sum} \,\,\Lambda \cdot B \cdot B\end{aligned}\]where operations $\cdot\,$, /, exp, and log are applied
cellwise, and $\textstyle\sum$ denotes the sum of all cells in a matrix.
The gradient of $f$ with respect to $B$ can be represented as a matrix
too:
The Hessian $\mathcal{H}$ of $f$ is a tensor, but, fortunately, the conjugate gradient inner loop of the trust region algorithm in [Lin2008] does not need to instantiate it. We only need to multiply $\mathcal{H}$ by ordinary matrices of the same size as $B$ and $\nabla f$, and this can be done in matrix form:
\[\mathcal{H}V \,\,=\,\, X^T \big( Q \,-\, P \cdot (Q\,1_{k\times k}) \big) \,+\, \Lambda \cdot V, \,\,\,\,\textrm{where}\,\,\,\,Q \,=\, P \cdot (XV)\]At each Newton iteration (the outer iteration) the minimization algorithm approximates the difference $\varDelta f(S; B) = f(B + S; X, Y) \,-\, f(B; X, Y)$ attained in the objective function after a step $B \mapsto B\,{+}\,S$ by a second-degree formula
\[\varDelta f(S; B) \,\,\,\approx\,\,\, (1/2)\,\,{\textstyle\sum}\,\,S \cdot \mathcal{H}S \,+\, {\textstyle\sum}\,\,S\cdot \nabla f\]This approximation is then minimized by trust-region conjugate gradient iterations (the inner iterations) subject to the constraint
\[\|S\|_2 \leq \delta\]The trust
region size $\delta$ is initialized as $0.5\sqrt{m}\,/ \max_i |x_i|_2$
and updated as described in [Lin2008].
Users can specify the maximum number of the outer
and the inner iterations with input parameters moi and
mii, respectively. The iterative minimizer terminates
successfully if
, where ${\varepsilon}> 0$ is a tolerance supplied by the user via input parameter tol.
Returns
The estimated regression parameters (the \(.\hat{\beta}_{j, l}\) ) are
populated into a matrix and written to an HDFS file whose path/name was
provided as the B input argument. Only the non-baseline
categories ($1\leq l \leq k\,{-}\,1$) have their $ \hat{\beta}{j, l}$
in the output; to add the baseline category, just append a column of zeros.
If icpt=0 in the input command line, no intercepts are used
and B has size
$m\times (k\,{-}\,1)$; otherwise
B has size
$(m\,{+}\,1)\times (k\,{-}\,1)$
and the
intercepts are in the
$m\,{+}\,1$-st row. If icpt=2, then
initially the feature columns in $X$ are shifted to mean${} = 0$ and
rescaled to variance${} = 1$. After the iterations converge, the
$\hat{\beta}{j, l}$’s are rescaled and shifted to work with the
original features.
Support Vector Machines
Binary-Class Support Vector Machines
Binary SVM Description
Support Vector Machines are used to model the relationship between a
categorical dependent variable y and one or more explanatory variables
denoted X. This implementation learns (and predicts with) a binary class
support vector machine (y with domain size 2).
Binary SVM Details
Support vector machines learn a classification function by solving the following optimization problem ($L_2$-SVM):
\[\begin{aligned} &\textrm{argmin}_w& \frac{\lambda}{2} ||w||_2^2 + \sum_i \xi_i^2\\ &\textrm{subject to:}& y_i w^{\top} x_i \geq 1 - \xi_i ~ \forall i\end{aligned}\]where $x_i$ is an example from the training set with its label given by $y_i$, $w$ is the vector of parameters and $\lambda$ is the regularization constant specified by the user.
To account for the missing bias term, one may augment the data with a
column of constants which is achieved by setting the intercept argument to 1
[Hsieh2008].
This implementation optimizes the primal directly [Chapelle2007]. It uses nonlinear conjugate gradient descent to minimize the objective function coupled with choosing step-sizes by performing one-dimensional Newton minimization in the direction of the gradient.
Binary SVM Returns
The learnt weights produced by l2-svm.dml are populated into a single
column matrix and written to file on HDFS (see model in section
Arguments). The number of rows in this matrix is ncol(X) if intercept
was set to 0 during invocation and ncol(X) + 1 otherwise. The bias term,
if used, is placed in the last row. Depending on what arguments are
provided during invocation, l2-svm-predict.dml may compute one or more
of scores, accuracy and confusion matrix in the output format
specified.
Multi-Class Support Vector Machines
Multi SVM Description
Support Vector Machines are used to model the relationship between a
categorical dependent variable y and one or more explanatory variables
denoted X. This implementation supports dependent variables that have
domain size greater or equal to 2 and hence is not restricted to binary
class labels.
Multi SVM Details
Support vector machines learn a classification function by solving the following optimization problem ($L_2$-SVM):
\[\begin{aligned} &\textrm{argmin}_w& \frac{\lambda}{2} ||w||_2^2 + \sum_i \xi_i^2\\ &\textrm{subject to:}& y_i w^{\top} x_i \geq 1 - \xi_i ~ \forall i\end{aligned}\]where $x_i$ is an example from the training set with its label given by $y_i$, $w$ is the vector of parameters and $\lambda$ is the regularization constant specified by the user.
To extend the above formulation (binary class SVM) to the multiclass setting, one standard approach is to learn one binary class SVM per class that separates data belonging to that class from the rest of the training data (one-against-the-rest SVM, see [Scholkopf1995]).
To account for the missing bias term, one may augment the data with a column of constants which is achieved by setting intercept argument to 1 [Hsieh2008].
This implementation optimizes the primal directly [Chapelle2007]. It uses nonlinear conjugate gradient descent to minimize the objective function coupled with choosing step-sizes by performing one-dimensional Newton minimization in the direction of the gradient.
Multi SVM Returns
The learnt weights produced by m-svm.dml are populated into a matrix
that has as many columns as there are classes in the training data, and
written to file provided on HDFS (see model in section Arguments). The
number of rows in this matrix is ncol(X) if intercept was set to 0
during invocation and ncol(X) + 1 otherwise. The bias terms, if used,
are placed in the last row. Depending on what arguments are provided
during invocation, m-svm-predict.dml may compute one or more of scores,
accuracy and confusion matrix in the output format specified.
Naive Bayes
Naive Bayes Description
Naive Bayes is very simple generative model used for classifying data. This implementation learns a multinomial naive Bayes classifier which is applicable when all features are counts of categorical values.
Naive Bayes Details
Naive Bayes is a very simple generative classification model. It posits that given the class label, features can be generated independently of each other. More precisely, the (multinomial) naive Bayes model uses the following equation to estimate the joint probability of a feature vector $x$ belonging to class $y$:
\[\text{Prob}(y, x) = \pi_y \prod_{i \in x} \theta_{iy}^{n(i,x)}\]where $\pi_y$ denotes the prior probability of class $y$, $i$ denotes a feature present in $x$ with $n(i,x)$ denoting its count and $\theta_{iy}$ denotes the class conditional probability of feature $i$ in class $y$. The usual constraints hold on $\pi$ and $\theta$:
\[\begin{aligned} && \pi_y \geq 0, ~ \sum_{y \in \mathcal{C}} \pi_y = 1\\ \forall y \in \mathcal{C}: && \theta_{iy} \geq 0, ~ \sum_i \theta_{iy} = 1\end{aligned}\]where $\mathcal{C}$ is the set of classes.
Given a fully labeled training dataset, it is possible to learn a naive
Bayes model using simple counting (group-by aggregates). To compute the
class conditional probabilities, it is usually advisable to avoid
setting $\theta_{iy}$ to 0. One way to achieve this is using additive
smoothing or Laplace smoothing. Some authors have argued that this
should in fact be add-one smoothing. This implementation uses add-one
smoothing by default but lets the user specify her/his own constant, if
required.
This implementation is sometimes referred to as multinomial naive Bayes. Other flavours of naive Bayes are also popular.
Naive Bayes Returns
The learnt model produced by naive-bayes.dml is stored in two separate
files. The first file stores the class prior (a single-column matrix).
The second file stores the class conditional probabilities organized
into a matrix with as many rows as there are class labels and as many
columns as there are features. Depending on what arguments are provided
during invocation, naive-bayes-predict.dml may compute one or more of
probabilities, accuracy and confusion matrix in the output format
specified.
Decision Trees
Decision Trees Description
Decision tree (for classification) is a classifier that is considered more interpretable than other statistical classifiers. This implementation is well-suited to handle large-scale data and builds a (binary) decision tree in parallel.
Decision Trees Details
Decision trees [BreimanFOS1984] are simple models of classification that, due to their structure, are easy to interpret. Given an example feature vector, each node in the learned tree runs a simple test on it. Based on the result of the test, the example is either diverted to the left subtree or to the right subtree. Once the example reaches a leaf, then the label stored at the leaf is returned as the prediction for the example.
Building a decision tree from a fully labeled training set entails choosing appropriate splitting tests for each internal node in the tree and this is usually performed in a top-down manner. The splitting test (denoted by $s$) requires first choosing a feature $j$ and depending on the type of $j$, either a threshold $\sigma$, in case $j$ is continuous-valued, or a subset of values $S \subseteq \text{Dom}(j)$ where $\text{Dom}(j)$ denotes domain of $j$, in case it is categorical. For continuous-valued features the test is thus of form $x_j < \sigma$ and for categorical features it is of form $x_j \in S$, where $x_j$ denotes the $j$th feature value of feature vector $x$. One way to determine which test to include, is to compare impurities of the tree nodes induced by the test. The node impurity measures the homogeneity of the labels at the node. This implementation supports two commonly used impurity measures (denoted by $\mathcal{I}$): Entropy $\mathcal{E}=\sum_{i=1}^{C}-f_i \log f_i$, as well as Gini impurity $\mathcal{G}=\sum_{i=1}^{C}f_i (1-f_i)$, where $C$ denotes the number of unique labels and $f_i$ is the frequency of label $i$. Once the impurity at the tree nodes has been obtained, the best split is chosen from a set of possible splits that maximizes the information gain at the node, i.e., $\arg\max_{s}\mathcal{IG}(X,s)$, where $\mathcal{IG}(X,s)$ denotes the information gain when the splitting test $s$ partitions the feature matrix $X$. Assuming that $s$ partitions $X$ that contains $N$ feature vectors into $X_\text{left}$ and $X_\text{right}$ each including $N_\text{left}$ and $N_\text{right}$ feature vectors, respectively, $\mathcal{IG}(X,s)$ is given by
\[\mathcal{IG}(X,s)=\mathcal{I}(X)-\frac{N_\text{left}}{N}\mathcal{I}(X_\text{left})-\frac{N_\text{right}}{N}\mathcal{I}(X_\text{right})\]where $\mathcal{I}\in{\mathcal{E},\mathcal{G}}$. In the following we
discuss the implementation details specific to
decision-tree.dml.
Input format. In general implementations of the decision tree algorithm do not require categorical features to be dummy coded. For improved efficiency and reducing the training time, our implementation however assumes dummy coded categorical features and dummy coded class labels.
Tree construction. Learning a decision tree on large-scale data has
received some attention in the literature. The current implementation
includes logic for choosing tests for multiple nodes that belong to the
same level in the decision tree in parallel (breadth-first expansion)
and for building entire subtrees under multiple nodes in parallel
(depth-first subtree building). Empirically it has been demonstrated
that it is advantageous to perform breadth-first expansion for the nodes
belonging to the top levels of the tree and to perform depth-first
subtree building for nodes belonging to the lower levels of the
tree [PandaHBB2009]. The parameter num_samples controls
when we switch to depth-first subtree building. Any node in the decision
tree that receives $\leq$ num_samples training examples,
the subtree under it is built in its entirety in one shot.
Stopping rule and pruning. The splitting of data at the internal nodes stops when at least one the following criteria is satisfied:
- the depth of the internal node reaches the input parameter
depthcontrolling the maximum depth of the learned tree, or - no candidate split achieves information gain.
This implementation also allows for some automated pruning via the
argument num_leaf. If a node receives $\leq$
num_leaf training examples, then a leaf is built in its
place.
Continuous-valued features. For a continuous-valued feature $j$ the
number of candidate thresholds $\sigma$ to choose from is of the order
of the number of examples present in the training set. Since for
large-scale data this can result in a large number of candidate
thresholds, the user can limit this number via the arguments
bins which controls the number of candidate thresholds
considered for each continuous-valued feature. For each
continuous-valued feature, the implementation computes an equi-height
histogram to generate one candidate threshold per equi-height bin.
Categorical features. In order to determine the best value subset to split on in the case of categorical features, this implementation greedily includes values from the feature’s domain until the information gain stops improving. In particular, for a categorical feature $j$ the $|Dom(j)|$ feature values are sorted by impurity and the resulting split candidates $|Dom(j)|-1$ are examined; the sequence of feature values which results in the maximum information gain is then selected.
Description of the model. The learned decision tree is represented in a matrix $M$ that contains at least 6 rows. Each column in the matrix contains the parameters relevant to a single node in the tree. Note that for building the tree model, our implementation splits the feature matrix $X$ into $X_\text{cont}$ containing continuous-valued features and $X_\text{cat}$ containing categorical features. In the following, the continuous-valued (resp. categorical) feature-ids correspond to the indices of the features in $X_\text{cont}$ (resp. $X_\text{cat}$). Moreover, we refer to an internal node as a continuous-valued (categorical) node if the feature that this nodes looks at is continuous-valued (categorical). Below is a description of what each row in the matrix contains.
- Row 1: stores the node-ids. These ids correspond to the node-ids in a complete binary tree.
- Row 2: for internal nodes stores the offsets (the number of columns)
in $M$ to the left child, and otherwise
0. - Row 3: stores the feature index of the feature (id of a
continuous-valued feature in $X_\text{cont}$ if the feature is
continuous-valued or id of a categorical feature in $X_\text{cat}$
if the feature is categorical) that this node looks at if the node
is an internal node, otherwise
0. - Row 4: store the type of the feature that this node looks at if the
node is an internal node:
1for continuous-valued and2for categorical features, otherwise the label this leaf node is supposed to predict. - Row 5: for the internal nodes contains
1if the feature chosen for the node is continuous-valued, or the size of the subset of values used for splitting at the node stored in rows 6,7,$\ldots$ if the feature chosen for the node is categorical. For the leaf nodes, Row 5 contains the number of misclassified training examples reaching at this node. - Row 6,7,$\ldots$: for the internal nodes, row 6 stores the threshold
to which the example’s feature value is compared if the feature
chosen for this node is continuous-valued, otherwise if the feature
chosen for this node is categorical rows 6,7,$\ldots$ store the
value subset chosen for the node. For the leaf nodes, row 6 contains
1if the node is impure and the number of training examples at the node is greater thannum_leaf, otherwise0.
As an example, Figure 2 shows a decision tree with $5$ nodes and its matrix representation.
Figure 2
Figure 2: (a) An example tree and its (b) matrix representation. $x$ denotes an example and $x_j$ is the value of the $j$th continuous-valued (resp. categorical) feature in $X_\text{cont}$ (resp. $X_\text{cat}$). In this example all leaf nodes are pure and no training example is misclassified.
(a) 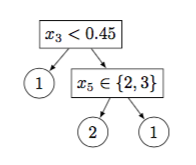
(b)
| Col 1 | Col 2 | Col 3 | Col 4 | Col 5 | |
|---|---|---|---|---|---|
| Row 1 | 1 | 2 | 3 | 6 | 7 |
| Row 2 | 1 | 0 | 1 | 0 | 0 |
| Row 3 | 3 | 0 | 5 | 0 | 0 |
| Row 4 | 1 | 1 | 2 | 2 | 1 |
| Row 5 | 1 | 0 | 2 | 0 | 0 |
| Row 6 | 0.45 | 0 | 2 | 0 | 0 |
| Row 7 | 3 |
Decision Trees Returns
The matrix corresponding to the learned model as well as the training
accuracy (if requested) is written to a file in the format specified.
See details where the structure of the model matrix is described. Recall
that in our implementation $X$ is split into $X_\text{cont}$ and
$X_\text{cat}$. If requested, the mappings of the continuous-valued
feature-ids in $X_\text{cont}$ (stored at S_map) and the
categorical feature-ids in $X_\text{cat}$ (stored at
C_map) to the global feature-ids in $X$ will be provided.
Depending on what arguments are provided during invocation, the
decision-tree-predict.dml script may compute one or more of
predictions, accuracy and confusion matrix in the requested output
format.
Random Forests
Random Forests Description
Random forest is one of the most successful machine learning methods for classification and regression. It is an ensemble learning method that creates a model composed of a set of tree models. This implementation is well-suited to handle large-scale data and builds a random forest model for classification in parallel.
Random Forests Details
Random forests [Breiman2001]
are learning algorithms for ensembles
of decision trees. The main idea is to build a number of decision trees
on bootstrapped training samples, i.e., by taking repeatedly samples
from a (single) training set. Moreover, instead of considering all the
features when building the trees only a random subset of the
features—typically $\approx \sqrt{D}$, where $D$ is the number of
features—is chosen each time a split test at a tree node is performed.
This procedure decorrelates the trees and makes it less
prone to overfitting. To build decision trees we utilize the techniques
discussed in Decision Trees and proposed
in [PandaHBB2009]; the implementation details are similar to those of
the decision trees script. Below we review some features of our
implementation which differ from decision-tree.dml.
Bootstrapped sampling. Each decision tree is fitted to a
bootstrapped training set sampled with replacement (WR). To improve
efficiency, we generate $N$ sample counts according to a Poisson
distribution with parameter subsamp_rate, where $N$
denotes the total number of training points. These sample counts
approximate WR sampling when $N$ is large enough and are generated
upfront for each decision tree.
Bagging. Decision trees suffer from high variance resulting in different models whenever trained on a random subsets of the data points. Bagging is a general-purpose method to reduce the variance of a statistical learning method like decision trees. In the context of decision trees (for classification), for a given test feature vector the prediction is computed by taking a majority vote: the overall prediction is the most commonly occurring class among all the tree predictions.
Out-Of-Bag error estimation. Note that each bagged tree in a random
forest model is trained on a subset (around $\frac{2}{3}$) of the
observations (i.e., feature vectors). The remaining ($\frac{1}{3}$ of
the) observations not used for training is called the
Out-Of-Bag (OOB) observations. This gives us a
straightforward way to estimate the test error: to predict the class
label of each test observation $i$ we use the trees in which $i$ was
OOB. Our random-forest-predict.dml script provides the OOB
error estimate for a given training set if requested.
Description of the model. Similar to decision trees, the learned
random forest model is presented in a matrix $M$ with at least 7 rows.
The information stored in the model is similar to that of decision trees
with the difference that the tree-ids are stored in the second row and
rows $2,3,\ldots$ from the decision tree model are shifted by one. See
Decision Trees for a description of the model.
Random Forests Returns
The matrix corresponding to the learned model is written to a file in
the format specified. See Decision Trees where the
details about the structure of the model matrix is described. Similar to
decision-tree.dml, $X$ is split into $X_\text{cont}$ and
$X_\text{cat}$. If requested, the mappings of the continuous feature-ids
in $X_\text{cont}$ (stored at S_map) as well as the
categorical feature-ids in $X_\text{cat}$ (stored at
C_map) to the global feature-ids in $X$ will be provided.
The random-forest-predict.dml script may compute one or
more of predictions, accuracy, confusion matrix, and OOB error estimate
in the requested output format depending on the input arguments used.